Erasure Coding Scheme for Data Protection and Recovery

Describes the erasure coding (EC) schemes for data protection and recovery.

Erasure coding (EC) is a data protection method in which data is broken into fragments, expanded and encoded with redundant data pieces, and stored across a set of different nodes or storage media.

EC ensures that if data becomes corrupted, it can be reconstructed using other data and parity fragments.

The time required to reconstruct data depends on the number of data fragments in the chosen EC scheme, and the number of failures that have occurred. For example, reconstruction of EC scheme 10+2 takes longer than the reconstruction of EC scheme 3+2, as a larger number of data and parity fragments must be read.

There are two kinds of EC schemes that you can use:

  • EC Schemes Without Local Parity: Even for a single failure, for a m+n scheme, the system must read a minimum of m other fragments to reconstruct data.
  • EC Schemes With Local Parity: In such schemes, data fragments are logically divided into groups with one local parity fragment per group, hence for a single failure the system reads just the remaining fragments in the affected group, along with the local parity fragment of the affected group, to rebuild data. Rebuilding data for a single failure is much faster on a scheme with a local parity, as a fewer number of fragments must be read.
NOTE
The value of parity fragment must be a non-zero positive number less than or equal to the number of data fragments.

Considerations When Selecting an EC scheme

As an administrator, consider the following points when selecting an EC scheme:

  • How many nodes can you afford to have?
  • How many failures might occur? Do you anticipate a single failure, or multiple failures?
  • Consider the following when determining how long you are willing to wait for a node to be rebuilt:
    • Rebuilds overhead - For 4+2, you need to read data from 4 nodes to rebuild, for 6+3, you need to read from 6 nodes to rebuild.
    • Reads overhead - For 4+2, you need to read data from 4 nodes, for 6+3, you need to read from 6 nodes. For degraded states, parity calculation overhead is an add-on.
    • Data classification - High ecschemes 10+2 , 12+4, are ideal for archived data, since data mostly remains untouched.

EC Schemes Without Local Parity

In an erasure coded volume, an erasure coding scheme without Local Parity has the stripe layout m+n. The stripe is an array of m data fragments and n parity fragments.

Each fragment is called a stripelet. ​Each stripelet is present on a container and one stripe is across different containers on different nodes.​ The default stripelet size is 4MB. For an EC scheme 4+2 for example, the stripe size is 24MB.

A Container Group (CG) is collection of such stripes. Based on the maximum size of a container (32 GB), the maximum number of stripes in a CG is 8K.

Each stripe is created by the same number of data fragments from all containers in the group of EC containers. Each container is placed on a different physical node.

  • m is the number of data fragments.
  • n is the number of redundant fragments (referred to as parity fragments).
  • The parity is calculated using data from all data fragments.
  • m/(m+n) is the encoding rate.
  • m+n is the number of encoded fragments.
  • You need to read a minimum of m blocks to recover data.
  • You can recover data from a maximum of n failures.

For example, assume m=4, n=2, and stripe depth=4 MB.



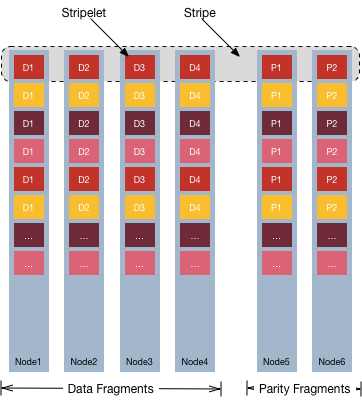
  • The number of data fragments is four (4), and while the number of parity fragments is two (2).
  • The number of encoded fragments is six (6).
  • The stripe size is 16 MB (4x4 MB) of user data, and 8 MB (2x4 MB) of parity fragments.
  • The system can handle two (2) failures, and any fragment can be recovered from four (4) other fragments.
Requirements for using an erasure coding scheme without local parity
  • The number of data fragments must be between 2 and 10 (both inclusive) for erasure coding scheme without local parity.
  • The number of nodes must be greater than or equal to the sum of data and parity fragments.
  • The number of parity fragments must be greater than or equal to 1 and less than or equal to the number of data fragments.

Select from the following schemes for erasure-coded volumes:

EC Scheme Number of Data Nodes Number of Parity Nodes Total Number of Nodes Needed Number of Failures Recoverable Number of Nodes to Read to Recover Data
2+2 2 2 4 2 2
3+2 3 2 5 2 3
4+2 4 2 6 2 4
5+2 5 2 7 2 5
6+3 6 3 9 3 6
10+<x> where x is a value from 1 to 10 10 x 10+x x 10

Although you can create a volume without the required number of nodes for a specific scheme, volume offload fails if the required number of nodes are not present.

When choosing the scheme, note that more nodes leads to longer recovery time, resulting in degraded performance, network expense, and lengthy time to rebuild.

If you anticipate only a single failure, use an EC scheme with local parity, as the number of nodes needed to be read for recovery is fewer, when compared to an EC scheme without local parity.

For example, consider a 12 + 4 EC scheme represented as D0 + D1 + D2 +....+D10 + D11 + P0 +…+P3​

Suppose node D4 goes down, now to rebuild, a total of 12 stripelets must be read.​ This leads to huge performance degradation in network bandwidth, CPU cycles, and Disk IO .

To reduce the reconstruction cost, use EC Local Parity, where the number of stripelets to be read reduces to 6 for a single failure in the 12+2+2 scheme.
IMPORTANT
The recommended number of nodes required for erasure coding is M+2N (rather than M+N) to ensure HPE Ezmeral Data Fabric self-healing and proper operation after N failures. N failures with only M+N nodes allows you to continue reading the data, but with significantly reduced performance because each read requires rebuilding data fragments. Also, manual intervention is required to protect the data from further failures. Currently, data will not be erasure coded if only M nodes are available. With M+2N nodes, N failures will self-heal with no operator intervention.

EC Schemes With Local Parity

Choosing an EC scheme with local parity, reduces EC storage overhead without incurring high rebuild costs and longer rebuild times while lowering the probability of data loss. Currently, the only supported local parity scheme is 6+2+2:

EC Scheme Number of Data Nodes Number of Local Parity Nodes Number of Global Parity Nodes Total Number of Nodes Needed Number of Failures Recoverable Number of Nodes to Read to Recover Data
6+2+2 6 2 2 10
  • 3 all the time
  • 4 most of the time
  • 3 for a single failure
  • 6 for multiple failures
The following technical discussion provides more information about local parity schemes.
IMPORTANT
The following discussion describes the 10+2+2 scheme for example purposes, but only the 6+2+2 local parity scheme is currently supported. For more information about specific parity schemes, contact HPE Support.

About Parity Schemes

Local parity is calculated from a subset of data blocks.

Consider a 10+2 scheme without local parity.

In this example, if block D6 fails, the system needs to read a minimum of 10 other blocks, to recover data.

Now consider a 10+2+2 scheme with local parity. In this case, data fragments are divided into two (2) data groups, each containing five (5) data fragments, with a local parity for each group. The global parity blocks are common to both data groups. To recover from a single failure, the system must read only the four (4) remaining fragments in the affected data groups, and the corresponding local parity fragment:

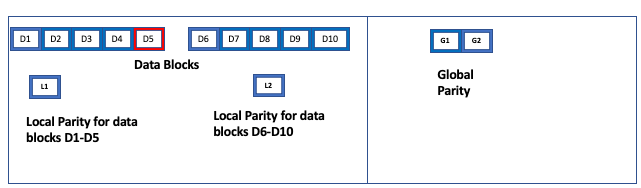
In this example, since there is only a single failure in a data group (block D5), the system must only read fragments D1+D2+D3+D4+L1 (which is the local parity fragment of this data group). Recovery is much faster and more efficient, due to the local parity block.

Points to note for using an erasure coding scheme with local parity

  • The number of data fragments must be between 2 and 16 (both inclusive) for erasure coding scheme with local parity.
  • In an EC scheme represented as k+g+l, k is the number of data blocks, g is the number of global parity blocks, and l is the number of local parity blocks.
  • You need k+g+l nodes for each local parity scheme.
  • k must be divisible by l to get k/l data fragments in each data group. For example, in the 10+2+2 EC scheme, there are 10/2=5 data fragments in each data group.
  • l must be greater than 1.
  • k must be greater than (g+l).
  • With local parity, the system can recover from 1 to g+1 failures at any time. In the 10+2+2 scheme, the system can recover from 1 to 3 failures at any time.
  • The system can recover from g+2 to g+l failures in certain cases. With the 10+2+2 scheme, the system can recover from 4 failures, in certain cases.
  • If none of the data fragments have failed in a data group, the system cannot use the corresponding local parity fragment, to recover from a failures in other data groups. For example:

    To recover D5, the system reads only D1+D2+D3+D4+L1. It does not read D1+D2+D3+D4+L2, since there are no failures in the data group D6 to D10, for which L2 is the local parity fragment.
  • For a single failure, the system needs to read k/l fragments to recover. For multiple failures, the system needs to read k fragments to recover.

With local parity, the system recovers from most of g+l failures. For the 10+2+2 scheme, the system can recover from most of 4 failures. For example:

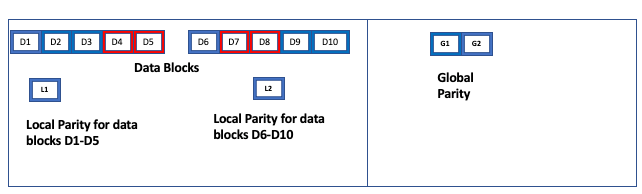
Here, there are 4 failures. The required number of blocks to read (10 in this case) are available, for recovery. The system reads D1+D2+D3+D6+D9+D10+L1+L2+G1+G2.

However, consider the following example:

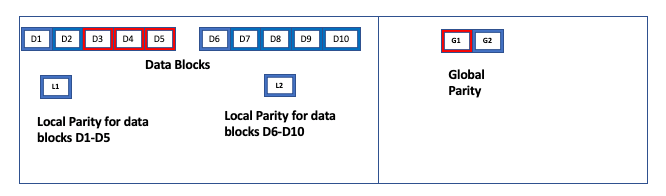
Although there are 4 failures, the system does not have the required number of fragments (10) to read and recover. The only fragments that can be read are D1+D2+L1+D6+D7+D8+D9+D10+G1. Fragment L2 cannot be read because there are no failures in its corresponding data group D6 to D10. Therefore in this case, data cannot be reconstructed.